Alumni

Bio
I am a rising senior from Austin, Texas, who likes to discover the inner workings of the universe, ranging from classical mechanics to quantum physics. Whenever I learn any concept, it is never enough to just have the formula; I must prove it to myself on the deepest level. When inspiration hits me, I can blather on for hours, even days, about Stokes' theorem, Maxwell's equations, or Euler's formula. When I am not studying mathematics, my hobbies include playing the clarinet, watching anime, reading manga, playing Dota 2, and practicing the esoteric art of pen spinning.
Project: The Hairy Ball Theorem
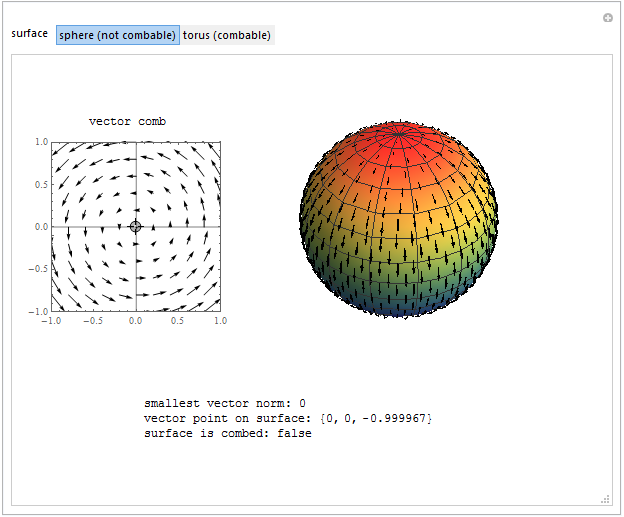
The hairy ball theorem states that for a sphere, or any homeomorphic surface, there is no continuous, nonvanishing tangent vector field—in other words, you cannot comb a hairy ball flat without at least one part or cowlick. In this Demonstration, a manipulatable vector field allows one to "comb" a tangent vector field on a sphere or torus, showing the point with the local minimum vector norm on that surface. If the smallest vector norm is zero, the hairy surface has a vanishing point, or "part," and is considered to be "not combed." On a sphere, this minimum point will always be zero for a tangent vector field, indicating a part, while a hairy torus can, in fact, be combed flat.