Alumni

Bio
I'm a 17-year-old Mexican high school student. I love music, and play piano and guitar; so far I've composed three pieces for piano. Also, I'm studying both Japanese and French, and I'm fluent in English and Spanish. I'm a black belt in Tae Kwon Do, and I practice tennis too. I like computers a lot, and I'm currently one of the last nine candidates for this year's Mexican Olympiad in Informatics delegation to be sent to the IOI (International Olympiad in Informatics). The final selection will take place the day after I return from the Mathematica Summer Research Program, so wish me luck!
Project: Binary Indexed Tree
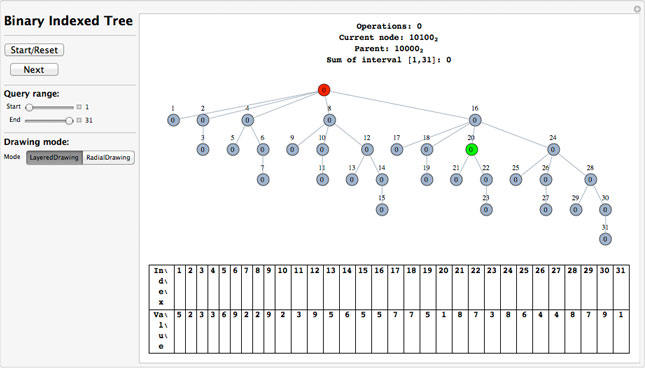
This is an implementation of a Binary Indexed Tree (also known as a Fenwick tree), a data structure used mainly for calculating prefix sums efficiently.
The prefix sum of a list in a certain index is the sum of all of the elements in the list up to that index, including itself. This algorithm speeds up the computation of prefix sums.
To use this Demonstration, drag the start and end sliders to the range you want to query and click the "Start/Reset" button. To proceed through the algorithm, use the "Next" button until the sum is correct.
Each node stores the sum of the interval (parent, node], so by starting at any node and adding up the values of all of the nodes on the way to the root, the sum of the interval [1, node] (its prefix sum) is computed. With this, to compute the sum of any given interval [n, m], it is only necessary to compute sum[1, m] - sum[1, n-1].
The tree is "binary indexed" because the parent of each node is obtained by removing the least significant bit from the node's index in base 2.
Queries can be executed with O(log N) time complexity after a one-time precomputation step, which takes O(N log N). If the array is modified, the tree can be updated in O(log N) time for each modified position.