Bio

Anjali Raj is a second-year undergraduate student of applied mathematics at the Indian Institute of Technology in Roorkee, India. Her academic interests include complex analysis, discrete mathematics, number theory and data structures, and algorithms. She is looking forward to exploring more of the Wolfram technologies in order to implement them in her studies and contribute to developing technologies in the field of mathematics. Apart from her academic interests, she likes traveling and photography.

Computational Essay

The RSA Algorithm »

Project: Algebraic Computations on Tropical Semirings

Goal

To implement and investigate arithmetic and matrix algebra over tropical semirings (min-plus and max-plus algebra) using the Wolfram Language and explore some of its applications.

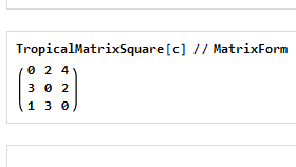
Main Results in Detail

I started with implementing the basic functions to compute linear algebra operations and then extended it for computing the general matrix operations over tropical semirings. Computational infeasibility (NP-hardness) of solving systems of linear equations in tropical algebra makes it a good candidate for key generation in an encryption algorithm, so I implemented the key generation function for cryptographic applications. Apart from that, I implemented an efficient method that finds the shortest path between two vertices in at most m steps for a given graph. The package I have developed for tropical semirings can be used for further exploration of the applications of tropical algebra.

Future Work

Since tropical algebra itself is a new branch of mathematics, much of its applications are not known to us. Due to the efficiency of matrix multiplication in tropical algebra, some interesting results for graph theory can be derived and possibly a deeper connection between graph theory and tropical algebra can be established. Other than graph theory applications, NP-hardness of solving systems of linear equations can be used as the basis for creating a much stronger cryptosystem than already exists. Now that we already have a package to implement tropical algebra, it will be much easier to investigate its other possible applications.