Bio

Austrian-born Michael received a Master of Business Administration for a thesis entitled, “Matsushita – Corporate Culture and Motivation in Japan”. He was awarded a PhD from Vienna University of Economics and Business Administration (WU) for a dissertation on support systems for university development. He has consulted for various entities and taught Marketing at WU from 1990 to 2001. Throughout his career he made many and various contributions to art events and systems conferences in Europe. For the last number of years he has engaged himself in NKS type research using Mathematica.

Project: Composition of Cellular Automaton Rules

The project report has nine sections: definition of the problem given by Stephen Wolfram and motives for choosing this open problem (1); remarks about the context of the project (2); preliminary findings illustrated by graphs and animations (3, 4, 5); an agenda for further research (6); notes (7); code examples (8); literature (9). The third section animates test results showing that 62 of the 256 elementary cellular automata can be decomposed into one or more combinations of range 1/2 automata, 96 combinations commute, two combinations return their initial conditions. The fourth section positions 2584 commuting substitutes for repeated applications of elementary rules and lists six combinations which return their initial conditions. The fifth section illustrates how the given prototype functions eliminate noise from the background of the three color neighborhood one automaton defined via rule number 6999927 by transforming it into a three color neighborhood four rule.

Favorite Three-Color Cellular Automaton

Rule Chosen: 5904187984162

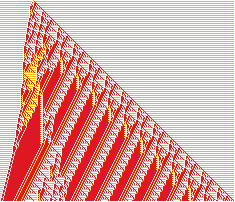
Reason: 5904187984162 was selected among other results of the random search because it features: uneven growth rates of left wing and right wing, obvious signs of class 4 behaviour (selective information transmission), and looks neither nested (class 2) nor purely random (class 3).

Additional Information

Schreiber, M. “Computational Equivalence: Spencer-Brown Form 110.” Presentation at NKS 2004, Boston, MA, 2004. [abstract] [materials]