Alumni

Aniruddh Sriram
Bio
Aniruddh is a rising senior at John Foster Dulles High School in Texas. He has a strong interest in mathematics and computer science and likes to engineer different Arduino projects and computer programs at home. He is the Director of the Dulles Computer Science Club, and he often gives club lectures and competes with his school's CS team at local UIL meets. Furthermore, he is also a USA Computing Olympiad (USACO) Platinum level contestant. In his free time, Aniruddh loves playing basketball and devouring North Indian "chaat" food.
Project: Investigating Pattern Periods in the Diagonals of the Rule 45 Cellular Automaton
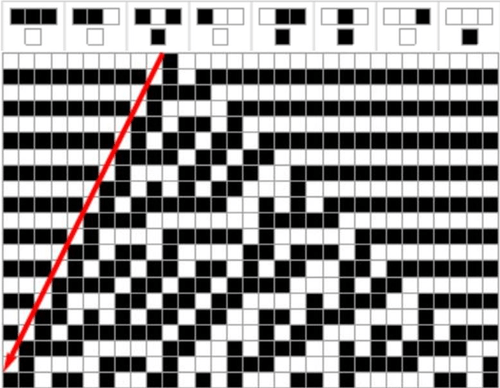
Goal
In this investigation, we examine the repetitive character of diagonal cells in the rule 45 cellular automaton. It is clear that along the left edge of the automaton, a pattern exists as the cells move diagonally downward. By moving further to the right (increasing the depth into the automaton), more patterns are detected with increasing periods. This phenomenon is seen in the rule 30 cellular automaton as periods seem to generally increase exponentially with increasing depth. This period doubling is truly an interesting occurrence, and we study the existence of similar repetitive behavior in rule 45. To analyze the developing patterns for especially longer sequences of cells, an efficient algorithm to detect patterns must be devised. After extracting long sequences of diagonal cells with increasing depth, we employ an algorithmic approach to evaluate the changes in period and examine this data to detect order in the increasing pattern periods.
Summary of Results
The results of the study indicated a clear ordered pattern in the periodicity of the diagonals. The first diagonal had a pattern periodicity of 1. As I extracted diagonals of slope 2 from the edge of the automaton, patterns were detected within the diagonals. The left side of the automaton looks relatively ordered and linear (as opposed to the more chaotic right side), and this qualitative observation is supported by the findings of this project. As one moves further into the automaton (toward the right), the diagonals attain pattern periods that progressively double. This period doubling is evident in the rule 30 elementary cellular automaton as well, and the fact that rule 45 exhibits similar behavior is quite interesting. Furthermore, at especially larger depths, there are long stretches of one unique period value until there is a change in period. The diagonal pattern values for the first 4000 diagonals are 1, 4, 8, 16, 32, 96, 192, etc. Another finding is that on the 46th diagonal, the periodicity triples from 32 to 96. This sudden period tripling is quite interesting since it follows a sequence of doubling (as opposed to tripling) periodicity. It is suspected that the periodicity doubling and tripling form their own pattern. Based on this, there may be another period tripling a lot deeper into the automaton at another diagonal.
Future Work
In the future, perhaps I can expand this project by delving deeper into the automaton. Using a machine with more processing power, I hope to generate more generations in my cellular automaton and analyze diagonals with higher depths and longer lengths. I want to investigate applications of nonlinear-feedback shift registers to my pattern data and possibly develop a formula or feedback function that can generate data about deeper diagonal patterns in polynomial time.