Alumni

Hedi Ben Daoud
Bio
Hedi Ben Daoud is a rising junior at the Pioneer High School of Bourguiba in Tunis. He spends most of his leisure time as a STEM enthusiast and part-time coder exploring the latest technological breakthroughs in several fields like artificial intelligence and quantum computing. He is also a member of the Tunisian national team for computing, an Intel International Science and Engineering Fair alumni for 2 editions, a speaker and a former member of different high school and science clubs. Hedi adores combining his competitive programming skills with mathematical thinking to come up with impactful projects and end-to-end solutions. He enjoys watching soccer games and taking his Jiu Jitsu classes.
Project: Captioning graphs of continuous functions
Goal
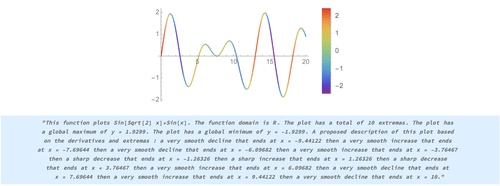
The project aims at extracting features from a function plot and expressing them using different representations to provide a consistent machine translation process. This work evaluates a function at different levels using a set of pre-built functions and mathematical methods. The extracted features are then mapped to a meaningful paragraph. A sonification function was implemented to audibly represent the graphs. The algorithms were tested on a set of functions and plots and showed the desired results for continuous polynomial and trigonometric functions. Different machine-learning algorithms were evaluated on a randomly generated dataset to classify curve plots. The machine-learning solution was able to generate a robust discriminative model despite the data scarcity.
Summary of Results
The designed program takes as input the function expression and explores a set of mathematical methods that evaluates the local and global extrema, the domain, the periodicity and the exponent. To extract these features, the algorithm evaluates the function at points where D[f[x],x]==0 and D[f[x],x,2]>=0 for maximums and D[f[x],x]==0 and D[f[x],x,2]<=0 for minimums within the predefined range. Based on the maximums and minimums of a given plot, the algorithm splits the function into intervals and samples these intervals over a list of points. By calculating the mean of the scaled derivative at each of these points and lower bounding it to the nearest threshold, the algorithm approximates the evolution of that function and its rate. A set of sentences were concatenated to produce a final meaningful paragraph. The heuristic approach demonstrated good results when tested with trigonometric and polynomial continuous functions. After sampling the points from a plot, magnifying the y values and wrapping them around a time series, AudioGenerator was used to map them to an audio signal for a duration t. The generated sounds showed a correlation between the actual plot and the audio signal. A machine-learning approach was followed to extend the results by further automating the process. An algorithm was developed to generate a set of random coefficients for quadratic and hyperbolic functions and their corresponding plots within a predefined x range. Three target classes were evaluated, ascending parabola, descending parabola and hyperbolic, using different classification models. There was no evidence of overfitting as the validation set tracked the training set during the training regimen.
Future Work
Extending this work to times series plots could have end-to-end impacts on a wide range of research fields. I think that generalizing these methods to other heuristic solutions in image captioning and integrating these techniques in a large platform for visually impaired people could provide a life-changing experience for them.