Alumni

Heidi Yoon
Bio
Heidi Yoon is a rising junior at Chadwick International School in South Korea. Her interests are mathematics, physics, and robotics. At Chadwick, she is the vice director and team leader for the school's VEX robotics club, which has multiple awards and experience at the VEX World Championship. Heidi also serves as a leader in the Chadwick Science Society, a club that runs science lessons with elementary school students, with a passion to encourage participation and interest of students in STEM. Apart from academics, Heidi is part of the varsity tennis team, and enjoys playing the piano, listening to music, and playing sports.
Project: Modeling the Orientation of a Random Polyhedron on Water
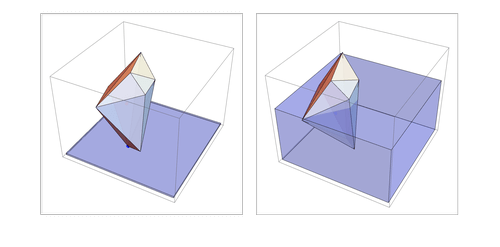
Goal
The objective of this project is to model the orientation at which a random polyhedron floats on water, through vertically aligning the center of buoyancy and center of gravity of the polyhedron. The resulting function would involve a system for the user to manipulate the density of the polyhedron and liquid, returning calculations for the center of buoyancy and center of gravity and a dynamic model that presents the polyhedron placed in water orienting itself.
Summary of Results
I was able to model one position of equilibrium for any random polyhedron and approximate the height the waterline would rise up to in the position of the polyhedron’s equilibrium by utilizing mainly the RegionCentroid function. The result had limitations in that only the horizontal displacement of center of gravity and center of buoyancy was taken into consideration, disregarding stability. Therefore, the resulting orientation of equilibrium may not correctly describe how an object reacts in actual water, as there may be more stable orientations based on the vertical position of center of gravity or metacenter.
Future Work
A potential extension for this project is to model all orientations in which a polyhedron is in equilibrium by running the code through a table of angles from 0 to 360 degrees and selecting the orientations in which the horizontal position of center of gravity and center of buoyancy match. Given a list of these values, I would make a function that determines the most stable equilibrium position by taking the metacenter and selecting the orientation in which the vertical position of the center of gravity is the lowest relative to the center of buoyancy. Also, for each random polyhedron, I would like to graph the angle at which the object is in equilibrium and the number of these equilibrium positions per each density ratio to generalize a pattern for the change in position of equilibrium for changes in density ratio.